En este post presento una manera de realizar la regresión de un mapa de compresor centrífugo mediante una polinomio multivariable de segundo grado empleando Scipy.

En ocasiones es necesario digitalizar los mapas de compresores centrífugos que son provistos por el fabricante a fin de predecir condiciones de operación del mismo.

Los mapas de compresores son importantes porque proveen información sobre los limites de operación de los compresores, definidos por la curva de surge y stonewall.

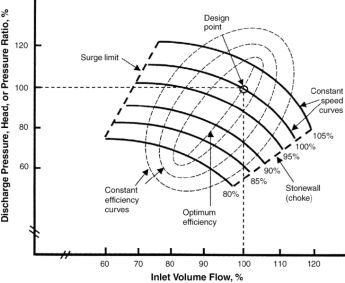
Donde cada una de las lineas negras continuas gruesas representan el lugar geométrico que la relación flujo volumétrico y presión de descarga a una velocidad de giro continuo.

1
2
3
4
5
6
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d
from matplotlib import cm
from scipy.optimize import curve_fit, least_squares

Curvas de desempeño según el fabricante

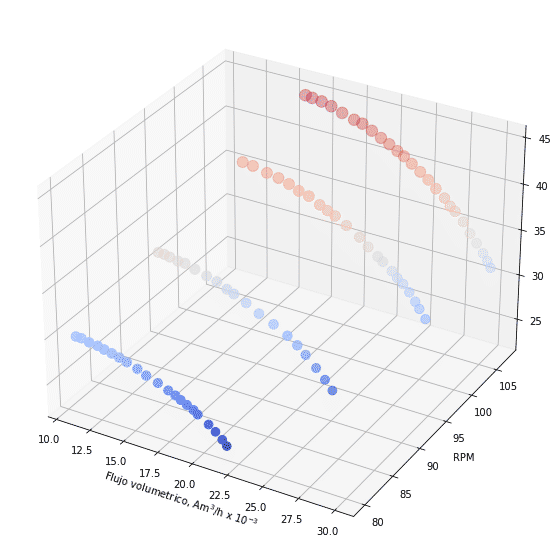
En primera instancia se reproducen los mapas de desempeño un compresor centrífugo genérico. Estas curvas fueron obtenidas directamente de las curvas aportadas por el OEM. En este ejemplo, el mapa provisto fue el de cabezal politrópico en función del caudal volumétrico actual de gas en unidades de Am3/h

Por cada mapa está conformado por 4 curvas a las siguientes velocidades de giro:

• 80% de velocidad de giro
• 90% de velocidad de giro
• 100% de velocidad de giro
• 107% de velocidad de giro

Los mapas suelen reportar las condiciones a las cuales fueron construidos dichos mapas. Como por ejemplo:

1
2
3
4
5
6
7
8
9
P1_OEM = 16.53          # Presion de succion, kg/cm2
T1_OEM = 39 + 273.15    # Temperatura de succion, K
P2_OEM = 37.35          # Presion de descarga, kg/cm2
T2_OEM = 135.2 + 273.15 # Temperatura de descarga, K
Q_OEM = 20684           # Flujo volumetrico, Am^3/h
M_OEM = 129722          # Flujo masico, kg/h
MW_OEM = 10.15          # Peso molecular
PH_OEM = 24702          # Cabezal politropico, kgm/kg
RPM_OEM = 10096         # Velocidad de giro, rpm

Cada curva se encuentra en archivos de texto.

1
2
3
4
5
6
7
8
9
10
folderMapas = "data_mapas/data_txt/"

# Curvas para el mapa de presion de descarga
df1stDP080 = np.loadtxt(folderMapas + 'K301-1st-DP080.txt', delimiter='\t', skiprows=1)
df1stDP090 = np.loadtxt(folderMapas + 'K301-1st-DP090.txt', delimiter='\t', skiprows=1)
df1stDP100 = np.loadtxt(folderMapas + 'K301-1st-DP100.txt', delimiter='\t', skiprows=1)
df1stDP107 = np.loadtxt(folderMapas + 'K301-1st-DP107.txt', delimiter='\t', skiprows=1)

# Reorganizacion de los datos
df1stDP = np.concatenate([df1stDP080, df1stDP090, df1stDP100, df1stDP107], axis=0)

Representación gráfica del mapa OEM

La representación gráfica de todas las curvas se hizo de la siguiente

1
2
3
4
5
6
7
8
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(1, 1, 1, projection='3d')

ax.scatter(caudal, rpm, P2, c=P2, s=P2*3, cmap=cm.coolwarm)
ax.set_ylabel('RPM ')
ax.set_xlabel('Flujo volumetrico, Am$^3$/h x 10$^{-3}$')
plt.savefig('performance_map.png', dpi=72, bbox_inches='tight')
plt.show()

Regresion de los mapas OEM

En la literatura se hace referencia que cada una de estas curvas puede ser modelada por polinomios de tercer grado y luego para conocer valores intermedios se realiza una regresion lineal.

Sin embargo, el Dr. Paparella en su artículo Load Sharing Optimization of Parallel Compressors (2013) Sugiere que se puede realizar la regresión del mapa mediante un polinomio multivariable de segundo grado. Este fue el approach seguido en este post.

De esta manera, las variables independientes serán caudal volumétrico y cabezal politrópico mientras que la variable dependiente será la velocidad de giro.

donde a, b, c, d, e y f son los coeficientes de ajuste, Q es el flujo volumétrico del gas, X representa la variable de proceso relativa al compresor y RPM representa la velocidad de giro del compresor. Estos parámetros son los que se ajustarán mediante la función curve_fit de scipy

Se crearon dos funciones auxiliares para la regresión:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def mapFit(x, a, b, c, d, e, f):
    '''
    regresion multivariable de los datos experimentales x
    output: a, b, c, d, e, f : coeficientes de regresion
    '''
    x1 = x[:,0]
    x2 = x[:,1]
    return a * x2 + b * x1 + c * x1 * x2 + d + e * x1**2 + f * x2**2

def fpredict(x1, y, coef, seed):
    '''
    funcion a minimizar empleando el metodo de minimos cuadrados.

    '''
    a, b, c, d, e, f = coef
    ftemp = lambda x2: y - (a * x2 + b * x1 + c * x1 * x2 + d + e * x1**2 + f * x2**2)
    return least_squares(ftemp, seed)

Comparación gráfica de los ajustes a los valores experimentales

Se crea vectores de flujo de gas que se encuentren entre los valores caudal de surge y stonewall para cada curva de velocidad de giro del compresor.

1
2
3
4
5
6
n_puntos = 100

Q080_val = np.linspace(min(df1stDP080[:,0]), max(df1stDP080[:,0]), n_puntos)
Q090_val = np.linspace(min(df1stDP090[:,0]), max(df1stDP090[:,0]), n_puntos)
Q100_val = np.linspace(min(df1stDP100[:,0]), max(df1stDP100[:,0]), n_puntos)
Q107_val = np.linspace(min(df1stDP107[:,0]), max(df1stDP107[:,0]), n_puntos)

Se realiza la predicción para cada una de las velocidad de rotación del compresor.

1
2
3
4
dp080 = [fpredict(X, 80, coefRpmDP1st, 27).x[0] for X in Q080_val]
dp090 = [fpredict(X, 90, coefRpmDP1st, 30).x[0] for X in Q090_val]
dp100 = [fpredict(X, 100, coefRpmDP1st, 35).x[0] for X in Q100_val]
dp107 = [fpredict(X, 107, coefRpmDP1st, 40).x[0] for X in Q107_val]

Reultados obtenidos

Se comparan los valores de presion de descarga calculados con respecto a los valores experimentales

Se evidencia una buena estimacion de los valores experimentales

Mas detalles sobre el código de resolución disponible en el siguiente enlace